Pagi ini saya mendapatkan Problem of The Day dari page Brilliant.org di facebook. Brilliant.org merupakan suatu website yang dibuat oleh Calvin Lin sebagai wadah atau komunitas untuk orang-orang yang tertarik dengan matematika. Masalah Matematika sederhana yang mereka berikan saat itu begini bunyinya:
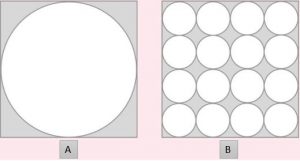
Perhatikan kedua gambar persegi A dan B di atas. Kira-kira persegi manakah yang memiliki luas lingkaran yang lebih besar ya? (dengan asumsi luas persegi A dan B adalah sama besar).
Mari kita bahas masalah tersebut di sini.
Luas lingkaran dalam persegi A
Misalkan panjang sisi persegi tersebut adalah 
, jadi jari-jari lingkarannya 
, maka kita punya
Luas lingkaran dalam persegi A = 
Luas semua lingkaran dalam persegi B
Karena panjang sisi perseginya , maka jari-jari dari masing-masing lingkaran adalah 
, jadi kita punya
Luas masing-masing lingkaran = 
.
Karena jumlah lingkarannya ada 
, maka
Luas semua lingkaran dalam persegi B = 
.
Jadi kesimpulannya luas lingkaran dalam persegi A sama besarnya dengan jumlah luas lingkaran-lingkaran yang ada di persegi B! 😀
Sumber Foto: Brilliant.org
0Baca Lagi Biar Pinter
- 54"Jika suatu lingkaran memiliki jari-jari sebesar $latex r=7 cm$, maka berapakah luas lingkaran tersebut?", tanya guru SD kita saat itu.…
- 51Ada dua ukuran yang digunakan ketika menghitung besar sudut: ukuran pertama adalah derajat yang sudah dikenal dengan baik sewaktu SD,…
- 46[latexpage] Soal-soal 0.3 Sistem Koordinat Rektangular Dalam soal-soal 1-4 gambarlah titik-titik yang diberikan dalam bidang koordinat dan kemudian carilah jarak…
- 42Coba teman-teman buat persegi dengan menggunakan korek api, kemudian miringkan sisi kanan dan kirinya ke sebelah kiri sehingga membentuk jajar…
- 41[Latexpage] Hari ini Shina ingin membuat sebuah wadah berbentuk kerucut yang dibentuk dari kertas berbentuk lingkaran dengan jari-jari sebesar $latex…
Leave a reply