Seberapa Jauh Kita dapat Menyusun Buku dengan Seimbang?

Send Message

Add post

Username* Please type your username .

E-Mail* Please type your E-Mail .

Post Title* Please choose an appropriate title for the post .

Category* Please choose the appropriate section so easily search for your post .

Tags Please choose suitable Keywords Ex : post , video .

Attachment

Browse

Details

Seberapa Jauh Kita dapat Menyusun Buku dengan Seimbang?

Bayangkan kita sedang bosan dan di sekitar kita terdapat banyak buku berserakan, yang mana buku-buku tersebut memiliki masa, bentuk, panjang dan lebar yang sama. Saking bosannya, kita ingin menyusun buku-buku tersebut menjadi seperti yang ada pada gambar berikut:

Sumber: sharepoint.umich.edu

Pertanyaan pun muncul di benak kita, kira-kira seberapa jauh ya buku-buku itu dapat kita susun dengan tetap seimbang, sehingga tidak ada satu pun buku yang jatuh? Sambil menyusun tumpukan bukunya, yuk kita juga sambil berkalkulus ria!

Sebelum menyusun bukunya, ada beberapa teori dasar yang harus kita ketahui terlebih dahulu, yakni mengenai pusat masa. Misalkan kita memiliki dua masa berukuran $m_{1}$ dan $m_{2}$ yang di letakkan pada papan jungkat-jungkit dengan masing-masing masa berjarak $d_{1}$ dan $d_{2}$ dari titik tumpu

Papan tersebut akan seimbang jika dan hanya jika $m_{1}d_{1}=m_{2}d_{2}$ . Jika permasalahan tersebut diletakkan pada garis koordinat mendatar dengan titik asal sebagai titik tumpu, maka koordinat $x_{1}$ dari $m_{1}$ adalah $x_{1}=-d_{1}$ , dan koordinat $x_{2}$ dari $m_{2}$ adalah $x_{2}=d_{2}$ .

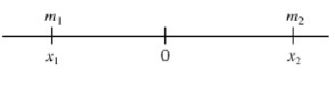
Kondisi keseimbangan akan terpenuhi jika $x_{1}m_{1}+x_{2}m_{2}=0$ . Kita juga dapat menentukan titik pusat dari kedua masa tersebut yang diberikan oleh persamaan

$\bar{x}= \frac{x_{1}m_{1}+x_{2}m_{2}}{m_{1}+m_{2}}$

Setelah mengetahui teori dasarnya, sekarang kita lanjutkan ke masalah sebelumnya, yakni menyusun buku sebanyak mungkin namun tetap dalam keadaan seimbang. Untuk memodelkannya, kita buat garis mendatar sehingga titik asalnya berada di ujung meja

Kita dapat asumsikan bahwa buku tidak akan terjatuh jika pusat masanya $\leq 0$ (artinya pusat masa dari buku tersebut harus berada di atas meja, tidak boleh melebihi atau keluar dari meja agar tidak jatuh). Sekarang kita coba menyusun satu-per-satu buku tersebut.

Langkah I: Misalkan diberikan panjang setiap bukunya adalah 2 dan masanya 1. Simpan buku pertama di atas meja sehingga ujung buku sebelah kanan terletak pada titik asal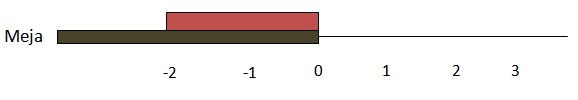

Kita punya pusat masanya adalah -1. Selanjutnya geserkan buku tersebut ke sebelah kanan sebesar 1 satuan sehingga pusat masanya menjadi 0, dan buku tersebut masih dalam keadaan seimbang di atas mejaPada langkah I diperoleh:

Masa satu buah buku: 1;

Pusat masa $\bar{x_{1}}=0$ ;

Panjang daerah yang menggantung $d_{1}=1$ .

Langkah II: Angkat buku pertama kemudian simpan buku kedua di bawahnya seperti pada gambar berikutPusat masa dari buku kedua adalah $x_{2}=-1$ , maka pusat masa dari kedua buku ini adalah

$\bar{x}=\frac{\bar{x_{1}}m_{1}+x_{2}m_{2}}{m_{1}+m_{2}}=\frac{0\cdot 1+(-1)\cdot 1}{1+1}=-\frac{1}{2}$

Selanjutnya geserkan kedua buku tersebut ke sebelah kanan sebesar 1/2 sehingga pusat masanya menjadi 0, dan kedua buku yang menggantung tersebut tetap dalam keadaan seimbang.Pada langkah II diperoleh:

Masa dua buah buku: 2;

Pusat masa $\bar{x_{2}}=0$ ;

Panjang daerah yang menggantung $d_{2}=1+\frac{1}{2}$ .

Langkah III: Kita angkat kembali kedua buku tersebut, kemudian simpan buku ketiga di bawahnya

Pusat masa buku ketiga adalah $x_{3}=-1$ , maka pusat masa dari ketiga tumpukan buku tersebut adalah

$\bar{x}=\frac{\bar{x_{2}}m_{2}+x_{3}m_{3}}{m_{2}+m_{3}}=\frac{0\cdot 2+(-1)\cdot 1}{1+2}=-\frac{1}{3}$

Selanjutnya kita geserkan ketiga buku tersebut ke sebelah kanan sebesar 1/3 sehingga pusat masanya menjadi 0.

Pada langkah III diperoleh:

Masa tiga buah buku: 3;

Pusat masa $\bar{x_{3}}=0$ ;

Panjang daerah yang menggantung $d_{3}=1+\frac{1}{2}+\frac{1}{3}$ .

Kita lakukan algoritma yang sama untuk menyusun buku-buku tersebut hingga n buah buku, sehingga diperoleh langkah ke-n sebagai berikut:

Langkah n: Asumsikan kita telah melakukan algoritma tersebut hingga menyusun n buah buku seperti pada gambar berikut

Misalkan banyaknya susunan n buku dinotasikan sebagai $s_{n}$ , yang memiliki pusat masa di 0 dan panjang daerah menggantung sebesar $d_{n}=1+\frac{1}{2}+\frac{1}{3}+\cdot\cdot\cdot+\frac{1}{n}$ . Karenanya untuk menyusun n+1 buku dapat dicari dengan langkah-langkah berikut:

Angkat tumpukan buku $s_{n}$ ke atas, kemudian simpan buku ke-n+1 di bawahnya, dengan ujung kanan tersebut terletak pada titik asal;
Simpan susunan $s_{n}$ buku tadi dengan buku yang baru, jadi kita punya susunan buku sebanyak n+1, atau dituliskan $s_{n+1}$ ;
Kita hitung pusat masa dari $s_{n+1}$ sebagai berikut

$\bar{x}=\frac{\bar{x_{n}}m_{n}+x_{n+1}m_{n+1}}{m_{n}+m_{n+1}}=\frac{0\cdot n+(-1)\cdot 1}{1+n}=-\frac{1}{n+1}$

Geserkan $s_{n+1}$ ke sebelah kanan sejauh $\frac{1}{n+1}$ sehingga pusat masanya berada di 0. Karenanya panjang daerah yang menggantung dari $s_{n+1}$ adalah $d_{n+1}=1+\frac{1}{2}+\frac{1}{3}+\cdot\cdot\cdot+\frac{1}{n+1}$ .

Berdasarkan iterasi yang telah kita lakukan sebelumnya, kita dapat menyusun buku sebanyak n dengan seimbang jika disimpan menggantung di atas meja, serta panjang daerah keseluruhan buku yang keluar melebihi meja adalah sebesar $d_{n}=1+\frac{1}{2}+\frac{1}{3}+\cdot\cdot\cdot+\frac{1}{n}= \sum_{k=1}^{n} \frac{1}{k}$ . Apa yang dapat kita simpulkan? Karena $\sum_{k=1}^{n} \frac{1}{k}$ merupakan jumlah parsial dari deret harmonik yang divergen, ini artinya kita dapat menyusun sebanyak apapun buku yang kita inginkan dengan keadaan yang seimbang! Jika panjang daerah yang melebihi meja adalah sebesar 2 satuan, maka kita membutuhkan 4 buah buku untuk disusun agar menjadi seimbang. Jika panjang daerah yang melebihi meja adalah sebesar 22 satuan, maka kita membutuhkan lebih dari 2 juta buku untuk disusun di atas meja agar menjadi seimbang, wow!

Ini merupakan hasil perhitungan secara teoritis, jika diaplikasikan langsung di dalam kehidupan nyata, maka kita harus benar-benar mencari buku ataupun benda sejenis dengan ukuran yang sama, serta harus kita susun dengan sangat hati-hati agar mendapatkan keseimbangan dan hasil yang menakjubkan~

Sumber: bigdatabbq.com

Referensi:

Series and Convergence. Interactive Real Analysis. Diakses 12 Desember 2017. [http://www.mathcs.org/analysis/reals/index.html]

How far can you overhang blocks?. DataGenetics. Diakses 11 Desember 2017. [http://datagenetics.com/blog/may32013/index.html]